Hoy llegamos al final de esta miniserie de lecciones sobre los intervalos en la música.
¿Te has perdido las lecciones anteriores? Pues no ha problema. Aquí puedes leer la primera, la cual sirve de introducción a los intervalos y sus diversas clasificaciones.
Introducción a los Intervalos en la Música
Y aquí puedes leer la segunda lección, donde explico sobre explico cómo se forma cada intervalo:
La Guía Definitiva de los Intervalos Musicales
Ahora que estamos familiarizados con los diversos tipos y clases de intervalos, es hora de aplicar este conocimiento identificando y construyendo intervalos. Para esto, detallaré en esta lección el proceso que personalmente uso al realizar estas tareas relacionadas con los intervalos.
Identificando Intervalos
Comencemos con la identificación de un intervalo previamente dado. Tomemos el siguiente como ejemplo:

En la imagen anterior podemos apreciar dos notas en el pentagrama: Fa sostenido y La.
Al identificar un intervalo, el primer paso es establecer qué tipo de intervalo es. Esto es lo que yo llamo establecer el “nombre” del intervalo. Para eso, debemos contar la cantidad de notas naturales contenidas entre las notas escritas en el pentagrama. Si obviamos por un momento las alteraciones que aparecen en la armadura (en este caso, el Fa sostenido), podemos ver que hay 3 notas contenidas, incluyendo la nota superior y la nota inferior. Estas tres notas son Fa – Sol – La. Por lo tanto, ya sabemos que el intervalo mostrado es una tercera.
¡Este primer paso es sumamente importante, y debe hacerse antes de lo demás! Un error que muchos estudiantes de teoría musical cometen al identificar intervalos es tratar de clasificar de primera instancia el intervalo contando los semitonos o tonos contenidos entre las notas dadas sin antes determinar qué tipo de intervalo es. Esto lleva al estudiante a cometer errores en el proceso de identificación y clasificación. Por esta razón, antes de contar semitonos y tonos, y buscar la clasificación del intervalo (si es mayor, menor, justo, disminuido o aumentado), es necesario establecer con claridad qué tipo de intervalo es (si es una tercera, cuarta, sexta, onceava, etc.) contando la cantidad de notas naturales contenidas, incluyendo la nota superior y la nota inferior. De esta manera se evita identificar y clasificar erróneamente el intervalo.
Una vez sabemos el “nombre” del intervalo (o sea, qué tipo de intervalo es) podemos ocuparnos de buscar el “apellido” (o sea, la clasificación del intervalo). Ya determinamos que el intervalo mostrado en la imagen anterior es una tercera, pues contiene tres notas naturales: Fa – Sol – La. Ahora veamos cuantos semitonos hay entre esas notas, para lo cual es necesario tomar en cuenta las alteraciones existentes. La primera nota es un Fa sostenido, y la segunda nota es un La. Al ascender desde Fa sostenido hasta La, encontramos que hay un total de 3 semitonos, o 1 tono y medio:
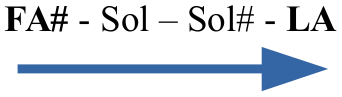
Por lo tanto, el intervalo mostrado es una tercera menor.
Repasemos el proceso utilizado para identificar el intervalo:
Contar la cantidad de notas naturales contenidas entre las notas dadas, incluyendo ambas, para determinar el “nombre” del intervalo. En este paso no prestamos atención a las alteraciones.
Contar la cantidad de semitonos o medios tonos al ascender (o descender, si fuera el caso) de una nota a otra para determinar el “apellido” del intervalo. En este paso sí tomamos en cuenta las alteraciones.
Veamos otro ejemplo, esta vez en Clave de Fa (Sí, sé que no se usa en la guitarra. Pero si quieres ser un músico completo, debes conocerla también):

Las notas mostradas son Sol y La bemol. Primeramente, contamos la cantidad de notas naturales que hay entre las notas —incluyendo ambas— sin prestar atención a las alteraciones:
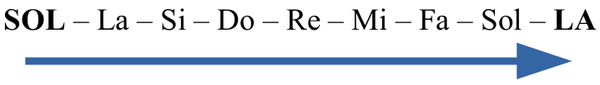
Entre Sol y La hay un total de nueve notas, así que se trata de un intervalo de novena. Pero ¿qué tipo de novena? Ahora contamos los semitonos (o tonos) para determinarlo:
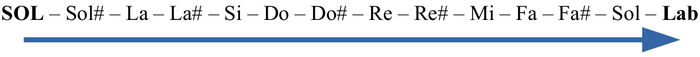
Entre Sol y La bemol hay 13 semitonos en total (6 tonos y medio), lo cual nos lleva a concluir que es un intervalo de novena menor.
Nuevamente, el proceso que utilice (y recomiendo seguir, para evitar errores) es:
- Contar la cantidad de notas naturales contenidas entre las notas dadas (sin prestar atención a las alteraciones; solo los nombres de las notas).
- Contar la cantidad de semitonos o medios tonos al ascender (o descender, si fuera el caso) de una nota a otra. En este paso sí tomamos en cuenta las alteraciones.
Si sigues estos pasos al pie de la letra, no tendrás problema alguno en identificar correctamente los intervalos.
Construyendo Intervalos
Al construir intervalos podemos aplicar un procedimiento similar al que utilizamos para identificar un intervalo dado:
- Se determina la nota que corresponde al “nombre” del intervalo y se escribe en el pentagrama. En este punto no prestamos atención a las alteraciones.
- Se determina la cantidad de tonos y/o semitonos necesarios para construir el intervalo y se añaden las alteraciones necesarias para lograr esa cantidad de tonos y/o semitonos.
Nada puede explicar este procedimiento mejor que un ejemplo. Veamos:
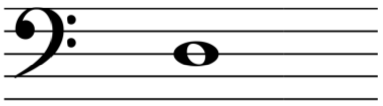
La imagen anterior ilustra una nota Re en Clave de Fa (sí, otro ejemplo en Clave de Fa, para que practiques 😀 ). A partir de esa nota vamos a construir un intervalo de tercera mayor ascendente. El primer paso es determinar la nota que corresponde al “nombre” del intervalo, así que no vamos a prestar atención a los tonos y semitonos por el momento. Lo primero que vamos a hacer en este punto es determinar qué nota está a una tercera de la nota Re. Contando tres notas mas arriba de Re encontramos la nota Fa:
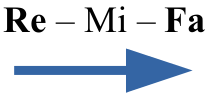
Por lo tanto, para hacer un intervalo de tercera a partir de la nota Re, lo primero que hacemos es escribir la nota Fa en el pentagrama:
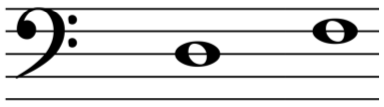
Una vez tenemos escrita la nota que corresponde al “nombre” del intervalo, ahora nos podemos ocupar del “apellido”. En este caso, el intervalo es una tercera mayor. Para que una tercera sea mayor, debe tener un total de 2 semitonos (2 tonos). Vamos a verificar qué distancia en semitonos (o tonos) hay entre Re y Fa:
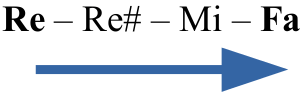
Entre Re y Fa hay un total de 3 semitonos (1 tono y medio), lo cual corresponde a una tercera menor. Por lo tanto, para construir una tercera mayor, necesitamos añadir un semitono adicional entre ambas notas. La nota Re —la nota original— no la podemos alterar ni cambiar, así que cualquier alteración necesaria debe realizarse en la nota añadida (la nota Fa). Para añadir el semitono necesario, basta con añadir a la nota Fa un sostenido, con lo cual obtenemos finalmente el intervalo de tercera mayor:

Sin temor a ser muy repetitivo, quiero recalcar nuevamente la importancia de escribir la nota que corresponde al “nombre” antes de contar los semitonos y/o tonos. Si contamos los semitonos primero, es posible que obtengamos lo siguiente:

La realidad es que entre Re y Sol bemol hay 4 semitonos, pues Sol bemol es enarmónico con Fa sostenido: Re – Re# - Mi – Fa – Sol bemol (Fa sostenido). Sin embargo, el intervalo ilustrado NO es una tercera mayor, aun cuando hay la misma cantidad de semitonos entra ambas notas. ¿Por qué? Porque entre las notas Re y Sol hay cuatro notas: Re – Mi – Fa – Sol. Por lo tanto, es un intervalo de una cuarta; específicamente, es un intervalo de cuarta disminuida. Al oído suenan igual —son enarmónicos— pero teóricamente son dos intervalos diferentes. Por eso es importante escribir la nota que corresponde al “nombre” antes de contar los semitonos y/o tonos (o sea, buscar el “apellido” del intervalo), de modo que se eviten errores como este.
Veamos otro ejemplo de construcción de un intervalo un poco mas complejo:

A partir de la nota Re, vamos a construir una onceava aumentada (o undécima aumentada). Antes de hacer cualquier otra cosa, determinamos la nota que corresponde al intervalo de onceava (sin prestar atención a los semitonos y/o alteraciones). Si contamos de forma ascendente 11 notas desde Re, encontramos que la nota correspondiente es Sol, ubicado justo arriba de la quinta línea:

Ahora que tenemos la nota que corresponde al intervalo de onceava, vamos a determinar cuántos semitonos (o tonos) se necesitan para una onceava aumentada. Ya sabemos que la onceava es un intervalo justo o perfecto; no existe una onceava mayor o menor. Por lo tanto, para obtener una onceava aumentada solo es necesario añadir un semitono (medio tono) a una onceava justa o perfecta. En el ejemplo anterior, tenemos una onceava justa, ya que hay un total de 17 semitonos (8 tonos y medio):

Por lo tanto, para obtener una onceava aumentada, es necesario aumentar medio tono a la nota Sol colocando un sostenido sobre la misma:

(Aunque no estamos hablando en sí de construcción de acordes, como nota adicional comento que este es el intervalo que se encuentra en acordes con #11, como por ejemplo C9#11).
Para terminar esta sección, repasemos el procedimiento para construir un intervalo desde cualquier nota dada:
- Se determina la nota que corresponde al “nombre” del intervalo y se escribe en el pentagrama. En este punto no prestamos atención a las alteraciones.
- Se determina la cantidad de tonos y/o semitonos necesarios para construir el intervalo y se añaden las alteraciones necesarias para lograr esa cantidad de tonos y/o semitonos.
Inversión de Intervalos Simples
Una destreza que es importante dominar al trabajar con los intervalos —en adición a identificarlos, clasificarlos y construirlos— es la inversión de los mismos. El saber invertir los intervalos correctamente es una destreza básica necesaria para poder entender tareas mas elaboradas como la inversión de acordes.
Para invertir un intervalo simple (una octava o menos de distancia entre ambas notas), la nota inferior del mismo se sube una octava, pasando a ocupar el rol de la nota superior. Por ejemplo, el intervalo armónico Mi – Sol

al invertirlo pasa a ser Sol – Mi, y Mi pasa a ser la nota superior:

También es posible invertir un intervalo simple bajando la nota superior una octava. El resultado es el mismo que subiendo la nota inferior, pero una octava mas abajo. En el siguiente ejemplo, el primer compás muestra un intervalo de segunda La – Si. En el segundo compás, el intervalo fue invertido subiendo la nota La una octava (flecha en color azul). En el tercer compás, el intervalo fue invertido bajando la nota Si una octava (flecha en color rojo). Fíjate cómo, en ambos casos, el resultado es un intervalo de séptima compuesto por las notas Si – La. La diferencia es que el resultado mostrado en el tercer compás está una octava mas grave:

Al invertir intervalos simples, siempre se dan las siguientes condiciones, la cuales nos permiten corroborar que la inversión haya sido hecha correctamente.
Si sumamos el número del intervalo original al número del intervalo invertido, el resultado siempre será 9. En el ejemplo anterior, Mi – Sol es un intervalo de tercera (3). Al invertirlo obtenemos Sol – Mi, lo cual corresponde a una sexta (6). La suma de 3 + 6 = 9. Por lo tanto, basándonos en esta condición podemos establecer lo siguiente:
- El unísono se convierte en una octava al invertirlo: 1 + 8 = 9.
- Una segunda se convierte en una séptima al invertirla: 2 + 7 = 9.
- Una tercera se convierte en una sexta al invertirla: 3 + 6 = 9.
- Una cuarta se convierte en una quinta al invertirla: 4 + 5 = 9.
- Una quinta se convierte en una cuarta al invertirla: 5 + 4 = 9.
- Una sexta se convierte en una tercera al invertirla: 6 + 3 = 9.
- Una séptima se convierte en una segunda al invertirlo: 7 + 2 = 9.
- Una octava se convierte en un unisono al invertirlo: 8 + 1 = 9.
Los intervalos menores se convierten en mayores. En el ejemplo anterior, Mi – Sol originalmente era una tercera menor. Al invertirla a Sol – Mi se convirtió en una sexta mayor.
Los intervalos mayores se convierten en menores. Por ejemplo, la segunda mayor Fa – Sol (primer compás) se convierte en la séptima menor Sol – Fa (segundo compás):

Los intervalos perfectos o justos se quedan igual. Por ejemplo, la cuarta perfecta Sol – Do (primer compás) se convierte en la quinta perfecta Do – Sol (segundo compás):
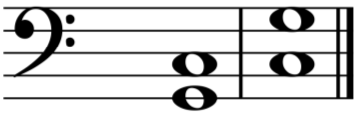
Los intervalos aumentados se convierten en disminuidos. Por ejemplo, la cuarta aumentada Fa – Si (primer compás) se convierte en la quinta disminuida Si – Fa (segundo compás):

Los intervalos disminuidos se convierten en aumentados. Por ejemplo, la tercera disminuida La – Do bemol (primer compás) se convierte en la sexta aumentada Do bemol – La (segundo compás):

Inversión de Intervalos Compuestos
Para invertir intervalos compuestos (mas de una octava de distancia entre las notas), bajamos la nota superior una octava, y subimos la nota inferior una octava. En otras palabras, primero convertimos el intervalo compuesto en su intervalo simple equivalente (bajando la nota superior una octava) y luego invertimos el intervalo como se explicó en la sección anterior.
En el ejemplo a continuación se muestra un intervalo de treceava (o decimotercera) mayor (notas Re – Si):

Para invertir este intervalo compuesto, primero bajamos la nota superior (Si) una octava para convertirlo en su intervalo simple equivalente. Eso nos deja con un intervalo de sexta mayor:

Finalmente, invertimos el intervalo subiendo la nota inferior (Re) una octava. Obtenemos como resultado una tercera menor (Si – Re):

Al invertir intervalos compuestos, siempre se dan las siguientes condiciones, la cuales nos permiten corroborar que la inversión haya sido hecha correctamente.
Si sumamos el número del intervalo original al número del intervalo invertido, el resultado siempre será 16. En el ejemplo anterior, Re – Si es un intervalo de treceava (13). Al invertirlo obtenemos Si – Re, lo cual corresponde a una tercera (3). La suma de 13 + 3 = 16. Por lo tanto, basándonos en esta condición podemos establecer lo siguiente:
- Una novena se convierte en una séptima al invertirla: 9 + 7 = 16.
- Una décima se convierte en una sexta al invertirla: 10 + 6 = 16.
- Una onceava se convierte en una quinta al invertirla: 11 + 5 = 16.
- Una doceava se convierte en una cuarta al invertirla: 12 + 4 = 16.
- Una treceava se convierte en una tercera al invertirla: 13 + 3 = 16.
Al igual que los intervalos simples:
- Los intervalos menores se convierten en mayores.
- Los intervalos mayores se convierten en menores.
- Los intervalos perfectos o justos se quedan igual.
- Los intervalos aumentados se convierten en disminuidos.
- Los intervalos disminuidos se convierten en aumentados.
Para finalizar, es importante notar que un intervalo compuesto se convierte en un intervalo simple al ser invertido. Sin embargo, un intervalo simple se convierte en otro intervalo simple al ser invertido.
Con esto terminamos esta lección y esta miniserie sobre los intervalos musicales. Estoy seguro que ayudara a disipar muchas dudas que puedas tener sobre este tema, e incluso a evitar que cometas algunos de los errores mas comunes al clasificar, identificar y construir intervalos.
¿Preguntas? Déjame saber en al sección de comentarios.
¡Éxito en tus estudios musicales!





Muy bien explicado y fácil. Gracias Ángel
Muchas gracias José. Me alegra que sea útil.
Ángel como se clasifican los intervalos?
Hola Paco.
Esto lo explico en la primera parte de esta lección, donde explico cómo identificar los intervalos. Si necesitas repasar sobre las diferentes clases de intervalos, te recomiendo echarle un vistazo a La Guía Definitiva de los Intervalos Musicales.
Saludos.
Muy buen trabajo sobre los intervalos. En general, la mayoría de las personas que tocan la guitarra como aficionados, e incluso muchos dedicados a la guitarra en niveles mas «profesionales» , no alcanzan a ver la importancia que tiene para conseguir un nivel adecuado de dominio de este instrumento, el conocimiento y práctica permanente de los intervalos, que son la base de los acordes y de la armonía, por lo que debemos utilizarlos con mucha mayor frecuencia en nuestras prácticas y actuaciones no solo para conseguir mejores resultados de interpretación, sino también para interpretar con mas seguridad y mucho mejor rendimiento.
Por todo ello, te agradezco el magnífico trabajo realizado, que sin lugar a dudas será de gran ayuda para todos los que amamos este bello, generoso y a la vez enigmático instrumento musical.
Hola Jorge.
Así es. Muchos se van por la «vía corta» y no aprecian la importancia que tiene la teoría musical y estos temas. Se quedan en saber tocar, pero no se ocupan en entender el porqué de lo que hacen.
Y no digo que tocar de oído sea malo. Al contrario; es importante saber tocar de oído también. Lo que digo es que, para ser un músico balanceado y mas completo, es necesario saber tocar de oído y también saber la teoría musical que explica lo que se está tocando. Eso es ser un músico completo.
Me alegra que personas como tú sepan apreciar la importancia del aspecto teórico en el estudio de la guitarra. Gracias por el aporte.
Saludos.
ANGEL TE PUEDO DECIR QUE LA LECCION ESTA MUY BIEN EXPLICADA. GRACIAS, TU AMIGO MARIO.
Gracias Mario.
Me alegra que sea de tu agrado.
Saludos.
bueno solo deseo muchas vendiciones por estas hermosas clases tan completas y mui vien explicadas,no hay para mi otro blok como este, tan bueo. sigue asi amigo y que dios le vendiga.
¡Wow, que halagador!
Muchas gracias por el comentario, Edgar. Es de mucha motivación para mí saber que mi trabajo es útil para otros.
Saludos.
muchas gracias por compartir tus conocimientos,soy una persona mayor que siempre quiso aprender a tocar guitarra con partituras, que Dios te bendiga por compartir tus dones.
Hola Fermin.
Un placer; me alegra que sea útil 🙂
Échale un vistazo a esta página donde recopilé las series de lecciones que he desarrollado. En ella hay una serie sobre cómo leer las notas en la guitarra que te puede ayudar a iniciarte en la lectura musical de partituras.
Y lo de ser mayor, eso es relativo. He visto jóvenes con un espíritu tan pobre que parecen que tienen 100 años, y gente «mayor» con un espíritu y actitud positiva que no hay quien los detenga. Si tienes el deseo y el compromiso, la edad no será impedimento. Todo está en ti 😉
Éxito con la guitarra.
Exelente trabajo maestro de maestros, es motivador para os que deseamos aprender a tocar guitarra, pero conociendola en su totalidad y usted explica para aprender eso y mas un abrazo
Me alegro que te motive, Tulio. Sigue adelante ????
Hola Ángel.
Siguiendo la regla de qué justo debajo de un traste está la cuarta de la tonica de arriba porque debajo de el primer traste de la sexta cuerda que es Fa hay un La sostenido si la cuarta sería un Si. Gracias
Hola Eloy.
No estoy seguro si entiendo bien el contexto de tu pregunta. En esta lección no muestro diagramas de notas o trastes en la guitarra, pues estoy hablando de distancia entre las notas y no posiciones en la guitarra.
Asumo (aunque no estoy seguro; me corriges si entendí mal) que te refieres a este diagrama:
Lo que sucede es que en ese diagrama realmente estoy contando la distancia entre las notas Fa y La en semitonos.
En realidad entre Fa y La no hay una cuarta, sino una tercera mayor. Quizás te has confundido porque viste que muestro 4 notas en la imagen, contaste 4 notas en total y asumiste que era una cuarta. Pero si te fijas bien hay 2 instancias de la nota Sol (una es natural y otra es sostenida) que para efectos de medir la distancia en intervalos cuentan como una nota. Esto lo explico en los párrafos que están justo antes de la imagen.
En nota aparte, ten en cuenta que la «regla» que comentas tiene una excepción muy importante: la 3ra. cuerda. Si pisas una nota en la 3ra. cuerda, la nota ubicada justo debajo en la 2da. cuerda no será una 4ta., sino una 3ra. mayor ?
Espero haber aclarado la duda. Si tienes alguna otra pregunta o no te ha quedado claro, siéntete en libertad de preguntar nuevamente.
Saludos.
Ángel Ángel Ángel. Zapatero a su Zapato. El error más común que encontramos es que la gente cree que porque una persona toca bien o muy bien un instrumento automáticamente es un buen maestro y puede enseñar a otros, eso está muy lejos de la verdad. Conozco a muchos buenos músicos, tremendos músicos, pero no son maestros. No saben explicar, no pueden… De cada 10, uno o dos son verdaderos maestros. Internet está lleno de buenos músicos, buenísimos, explicando una cosa y loque hacen es enredar más a uno ?????. Da rabia. Hahahahaaa.
ÁNGEL UD ES UN MAESTRO. UN VERDADERO MAESTRO. MIS FELICITACIONES.
Conchale porfin encontré a un maestro que me explico eso de los intervalos tan claro que pude comprender. Tremendo Ángel. Tremendo. Ud. tiene la vocación. No se como tocas, pero de que eres maestro “ERES”.
Mis felicitaciones una vez más y muchas muchas gracias.
Muy buenas José.
Hombre, me has hecho el día con tan motivador comentario. Muchas gracias. Me alegro mucho de que la explicación haya sido útil y clara para ti.
En realidad no me considero un gran guitarrista. Creo que toco bien, pero nada impresionante. Pero la verdad es que, si pudiera escoger la manera en la cual sea recordado luego de morir, prefiero ser recordado como un buen maestro que realmente dio el máximo por sus estudiantes, que un gran músico. Iría a la tumba feliz si eso se cumple, y por ello me esfuerzo cada día.
Nuevamente gracias, porque comentarios como el tuyo me dicen que voy por buen camino 🙂 Un placer haber sido de ayuda.
Éxito.
Soy principiante en esto de intervalos y necesito hacer el intervalo de Re 6ta Mayor y Fa# (sostenido) pero no tengo idea de cómo construir el intervalo, agradecería una ayuda por favor
Hola Sofía.
Perdona, no estoy seguro de entender bien tu pregunta. A ver, ¿desde qué nota necesitas hacer un intervalo de sexta mayor? ¿Desde Re o desde Fa#?
Hola, si es desde Fa#
Una sexta mayor a partir de Fa# es Re#.
Te recomiendo leer también La Guía Definitiva de los Intervalos Musicales. Creo que puede ayudarte a entender cómo se construyen los intervalos.
Éxito.
muchas gracias me ayudo mucho y mas que todo con los tetracordios y las escalas mayores,menores naturales, menores armonicas y menores melodicas. soy clarinetista.
Me alegro que haya sido útil, Verónica. La teoría musical es universal y aplica a todo instrumento.
Éxito.
me puedes decir por favor si el intervalo de 2da fa a sol tiene un tono
Buenas Luisa.
Sí, de Fa a Sol hay un intervalo de 1 tono. Los únicos pares de notas naturales que de por sí están a medio tono son Mi – Fa y Si – Do. Las demás notas naturales están a 1 tono.